Математика. Факультатив по подготовке к ОГЭ.

Урок № 21.

Тема: Декартовы координаты на плоскости.

    Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения. Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет.

Понятие декартовой системы координат

Если вы находитесь в некоторой нулевой точке и размышляете над тем, сколько единиц расстояния нужно пройти строго вперёд, а затем - строго вправо, чтобы оказаться в некоторой другой точке, то вы уже пользуетесь прямоугольной декартовой системой координат на плоскости. А если точка находится выше плоскости, на которой вы стоите, и к вашим расчётам добавляется подъём к точке по лестнице строго вверх также на определённое число единиц расстояния, то вы уже пользуетесь прямоугольной декартовой системой координат в пространстве.

Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат.

С именем французского математика Рене Декарта (1596-1662) связывают прежде всего такую систему координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми. Помимо прямоугольной существует общая декартова система координат (аффинная система координат). Она может включать и не обязательно перпендикулярные оси. Если же оси перпендикулярны, то система координат является прямоугольной.

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве - три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат - чисел в соответствии единице длины системы координат.

Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy и находящейся выше этой плоскости на 3 единицы.

С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a; b) удовлетворяют уравнению (x - a)² + (y - b)² = R².

Прямоугольная декартова система координат на плоскости

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости. Одна из этих осей называется осью Ox, или осью абсцисс, другую - осью Oy, или осью ординат. Эти оси называются также координатными осями. Обозначим через Mx и My соответственно проекции произвольной точки М на оси Ox и Oy. Как получить проекции? Проведём через точку М прямую, перпендикулярную оси Ox. Эта прямая пересекает ось Ox в точке Mx. Проведём через точку М прямую, перпендикулярную оси Oy. Эта прямая пересекает ось Oy в точке My. Это показано на рисунке ниже.




Декартовыми прямоугольными координатами x и y точки М будем называть соответственно величины направленных отрезков OMx и OMy. Величины этих направленных отрезков рассчитываются соответственно как x = x0 - 0 и y = y0 - 0. Декартовы координаты x и y точки М называются соответственно её абсциссой и ординатой. Тот факт, что точка М имеет координаты x и y, обозначается так: M(x, y).

Координатные оси разбивают плоскость на четыре квадранта, нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.

Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой - в уроке полярная система координат.




Прямоугольная декартова система координат в пространстве

Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве.

Одну из указанных осей называют осью Ox, или осью абсцисс, другую - осью Oy, или осью ординат, третью - осью Oz, или осью аппликат. Пусть Mx, My Mz - проекции произвольной точки М пространства на оси Ox, Oy и Oz соответственно.

Проведём через точку М плоскость, перпендикулярную оси Ox. Эта плоскость пересекает ось Ox в точке Mx. Проведём через точку М плоскость, перпендикулярную оси Oy. Эта плоскость пересекает ось Oy в точке My. Проведём через точку М плоскость, перпендикулярную оси Oz. Эта плоскость пересекает ось Oz в точке Mz.




Декартовыми прямоугольными координатами x, y и z точки М будем называть соответственно величины направленных отрезков OMx, OMy и OMz. Величины этих направленных отрезков рассчитываются соответственно как x = x0 - 0, y = y0 - 0 и z = z0 - 0.

Декартовы координаты x, y и z точки М называются соответственно её абсциссой, ординатой и аппликатой.

Попарно взятые координатные оси располагаются в координатных плоскостях xOy, yOz и zOx.

 https://function-x.ru/geometry_coordinates_cartesian.html






Урок № 20.

Тема: Числовые функции.

      Если даны числовое множество X и правило f, позволяющее поставить в соответствие каждому элементу x из множества X определённое число y, то говорят, что задана функция y=f(x) с областью определения X.

Областью определения функции y=f(x)  называют множество всех значений x, для которых функция имеет смысл. 

Множество всех значений функции y=f(x), x∈X, называют областью значений функции.

Пишут: y=f(x),x∈X,

x — независимая переменная (аргумент);

y — зависимая переменная;

D(f) — область определения функции;

E(f) — область значения функции.

Задать функцию — это значит указать правило, которое позволяет по произвольно выбранному значению  x∈D(f) вычислить соответствующее значение y.

Способы задания функции:

1. Графический: функция задаётся графиком.

Если дана функция y=f(x),x∈X, и на координатной плоскости xOy отмечены все точки вида (x;y), где x∈X, а y=f(x), то множество этих точек называют графиком функции y=f(x),x∈X.

2. Аналитический: функция задаётся формулой.

https://www.yaklass.ru/p/algebra/9-klass/chislovye-funktcii-svoistva-chislovykh-funktcii-9132/opredelenie-chislovoi-funktcii-i-sposoby-ee-zadaniia-9178/re-fb9aff63-201e-45b0-be39-f964ef64cc77

Давайте рассмотрим некоторые примеры:

1.       Область определения функции y=√xy=x является D(f)=[0;+∞)D(f)=[0;+∞), поскольку квадратный корень мы можем извлекать только из неотрицательного числа.
Часто не указывают область определения, тогда подразумевается, что она совпадает с исходным выражением.

2. Найти область определения функции: y=√x2+2x+1y=x2+2x+1.
Решение. Область определения не указана, значит она совпадает с область определения исходного выражения.
y=√x2+2x+1=√(x+1)2y=x2+2x+1=(x+1)2 – значит, наша функция определена при всех значения х.
Тогда D(f)=(- ∞;+∞).

3. Найти область определения функции: y=√x2+3x+2y=x2+3x+2.
Нам надо решить неравенство x2+3x+2>0x2+3x+2>0, т.к. выражение, содержащее корень, имеет смысл только при неотрицательном выражении под корнем.
(x+2)(x+1)>0(x+2)(x+1)>0,
Решим неравенство методом интервалов:

Тогда областью определения будет D(f)=(−∞;−2)U(−1;+∞)D(f)=(−∞;−2)U(−1;+∞).

Область значений числовых функций:


Также важное понятие, связанное с функциями - это область значений функции.

Область значения функции – это все значения, которые может принимать y=f(x)y=f(x), хϵХ. Обозначается как E(f).

Например, областью значений функции y=√xy=x будет промежуток (0;+∞]. E(√x)=(0;+∞]E(x)=(0;+∞].
Графиком функции y=f(x)y=f(x), хϵХ называется множество F точек координатной плоскости xОy: F={(x;y)|xϵX,y=f(x)}.

Если известен график функции, то область значений найти нетрудно, достаточно посмотреть: какую область значений по координате у принимает наша функция.
Пусть у нас задана некоторая функция y=f(x)y=f(x), график которой изображен ниже:


По графику видно, что у изменяется о


т -3 до +3. Тогда область значений функции Е(у)=[−3;3].Е(у)=[−3;3].

https://mathematics-tests.com/9-klass-uroki-prezentatsii-obzor/algebra-9-klass-chislovye-funktsii


Свойства числовых функций:

 

Функцию y=f(x) называют возрастающей на множестве X⊂D(f), если для любых точек x1 и x2 множества X — таких, что x1<x2 — выполняется неравенство f(x1)<f(x2).

 Функцию y=f(x) называют убывающей на множестве X⊂D(f), если для любых точек x1 и x2 множества X — таких, что x1<x2 — выполняется неравенство f(x1)>f(x2).

Иными словами:

функция возрастает, если большему значению аргумента соответствует большее значение функции;

функция убывает, если большему значению аргумента соответствует меньшее значение функции.

Исследование функции на ограниченность

Функцию y=f(x) называют ограниченной снизу на множестве X⊂D(f), если все значения этой функции на множестве X больше некоторого числа; иными словами, если существует число m — такое, что для любого значения x∈X выполняется неравенство f(x)>m.

Функцию y=f(x) называют ограниченной сверху на множестве X⊂D(f), если все значения этой функции на множестве X меньше некоторого числа; иными словами, если существует число M — такое, что для любого значения x∈X выполняется неравенство f(x)<M.

Наименьшее и наибольшее значения функции:

Число m называют наименьшим значением функции y=f(x) на множестве X⊂D(f), если

1) существует точка x0∈X, такая, что f(x0)=m;

2) для любого значения x∈X выполняется неравенство f(x)≥f(x0).

 

Число M называют наибольшим значением функции y=f(x) на множестве X⊂D(f), если

1) существует точка x0∈X, такая, что f(x0)=M;

2) для любого значения x∈X выполняется неравенство f(x)≤f(x0).

Обозначения:

yнаим — наименьшее значение функции;

yнаиб — наибольшее значение функции.

Если функция имеет  наибольшее значение yнаиб, то её называют ограниченой сверху.

Если функция имеет наименьшее значение yнаим, то её называют ограниченной снизу.

Соответственно, можно рассуждать наоборот.  Если функция не ограничена сверху, то у неё не существует наибольшего значения yнаиб. И если функция не ограничена снизу, то у неё не существует наименьшего значения yнаим.

Нули функции

Нулём функции y=f(x) называется такое значение аргумента x0, при котором функция обращается в нуль.

 https://www.yaklass.ru/p/algebra/9-klass/chislovye-funktcii-svoistva-chislovykh-funktcii-9132/svoistva-osnovnykh-funktcii-9106/re-059ef633-ae82-44dd-a3b5-1b1a78cd3288





Урок № 18 - 19.

Тема: Сложные проценты.

    Для инвестора сложный процент – это основной инструмент, который помогает максимально быстро приумножать доходы. 

Что такое сложный процент:

Это «процент на процент». То есть когда на какую-то сумму начисляется процент, второй процент считается уже не от первой суммы, а от увеличенной. Проще всего это разобрать на примере.

Пример:

Вы положили в банк миллион. Условия вклада: ежегодно начисляется 10 % на депозит, процент сложный.

Через год вы получите 10 % на свой миллион. То есть сто тысяч.

А еще через год 10 % уже будут считаться от увеличенной суммы, то есть от миллиона и ста тысяч. И получите вы 110 тысяч рублей, а не 100.

Если бы процент у вас был простым, то вы в первый год получили бы сто тысяч и во второй сто тысяч. Через два года ваш доход был бы на десять тысяч рублей меньше.


Плюсы и минусы сложного процента:

Его главный плюс в том, что деньги начинают приумножаться быстрее. Вы как бы наращиваете скорость своего обогащения, постоянно подпитываете инвестиционный портфель.

Минусов два. Первый – вы не получаете деньги на руки, не тратите их на себя. И не можете себя побаловать никакими плюшками.
Второй минус. Если вы делаете рискованные инвестиции и не защищаете их, вы можете потерять свои деньги. Или на несколько лет уйти в минус. Например, из-за кризиса.

А0 – первоначальное значение величины,

р – количество процентов,

n – количество расчетных периодов,

Аn – конечное значение величины.



Истекший период

«Простые проценты»

«Сложные проценты»

1 год

110=100+0,1×100

110=100+0,1×100

110=100 × (1+0,1)

2 года

120=110+0,1×100

120=100+2×0,1×100

121=110+0,1×110

121=110 × (1+0,1)

121=100 × (1+0,1)2

3 года

130=100+3×0,1×100

133=100 × (1+0,1)3

4 года

140=100+4×0,1×100

146=100 × (1+0,1)4

5 лет

150=100+5×0,1×100

161=100 × (1+0,1)5

…

…

…

n лет


https://infourok.ru/urok-algebry-v-9-klasse-prostye-i-slozhnye-procenty-5107397.html



Пример 1. Вкладчик положил на депозит $ 3000 под 9% годовых на 10 лет. Какая сумма аккумулируется конце 10-го года при годовой капитализации? На сколько вырастет сумма по сравнению с первоначальным взносом?

Решение: Применяем формулу сложных процентов для нахождения суммы в конце срока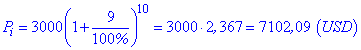
сложные проценты, вычисления
Чтобы ответить на второй вопрос, от значения 7102,09 вычитаем сумму вклада.

Разница составляет 4102 доллара.

 

Пример 2. Инвестор вложил 7000 грн под 10% годовых при условии начисления сложных процентов ежеквартально. Какую сумму он получит через 8 лет?

Решение: Применяем 2 формулу сложных процентов. Находим количество кварталов
8*4=32.
и подставляем в формулу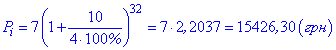
сложные проценты, вычисления

https://yukhym.com/ru/matematika/slozhnye-protsenty-na-primerakh.html




Урок № 16 - 17.

Тема: Числовые последовательности.

Функцию y=f(x), x∈N, называют функцией натурального аргумента, или числовой последовательностью, и обозначают y=f(n), или y1,y2,y3...yn...

Значения y1,y2,y3...yn — члены последовательности: первый, второй, третий (и т. д.).

 

В записи yn число n — индекс, задающий порядковый номер члена последовательности. Альтернативным вариантом обозначения последовательности является запись (yn).

Мы знакомы с различными способами задания функции: аналитический, графический, табличный, словесный. Для задания последовательностей особое внимание следует уделить следующим способам задания: аналитический, словесный и рекуррентный.

1. Аналитическое задание последовательности.

Чтобы задать последовательность аналитически, необходимо указать формулу её n-го члена yn=f(n).

Пример:

1. yn=n3.

Продемонстрирован аналитический способ задания последовательности 1,8,27,64... n3..., о которой шла речь выше.

2. Словесное задание последовательности.

Пример:

последовательность простых чисел: 2,3,5,7,11,13,17,19,23,29...

Последовательность задана словесно.

Данный способ задания последовательности не всегда эффективен, т. к. бывает очень сложно по словесному описанию найти аналитическое представление последовательности.

3. Рекуррентное задание последовательности.

Даётся формула или правило для вычисления n-ого члена последовательности через предыдущий (n−1)-ый член.

Так, второй член последовательности мы можем рассчитать по первому, третий — по второму и т. д.. Данный способ задания последовательности называют рекуррентным (от лат. recurrere — возвращаться).

Зачастую в таких случаях записывают формулу, позволяющую выразить n-й член последовательности через предыдущие, и задают первые два члена последовательности.

Пример:

y1=2;yn=yn−1+3, если n=2,3,4...

Имеем

y1=2;y2=y1+3=2+3=5;y3=y2+3=5+3=8;y4=y3+3=8+3=11и т.д.

https://www.yaklass.ru/p/algebra/9-klass/chislovye-posledovatelnosti-progressii-9139/poniatie-chislovoi-posledovatelnosti-sposoby-zadaniia-posledovatelnostei-11943/re-267fbf41-3e8d-4528-a23c-bc835806a480

 Виды последовательностей: 










Принцип математической индукции:



https://100urokov.ru/predmety/urok-6-chislovye-posledovatelnosti

Развитие учения о прогрессиях

Слово «прогрессия» латинского происхождения (progressio), бук­вально означает «движение вперед» (как и слово «прогресс»). И встречается впервые у римского автора Боэция (V-VI вв.). Пер­воначально под прогрессией понимали всякую числовую после­довательность, построенную по закону, позволяющему неограни­ченно продолжать ее в одном направлении, например последова­тельности натуральных чисел, их квадратов и кубов.

О том, как давно была известна геометрическая прогрессия, свидетельствуют папирусы Ахмеса.

Возможно, что древние вавилоняне и другие народы той дале­кой эпохи имели некоторые общие приемы решения задач, которые дошли до нас, однако об этих приемах мы пока ничего не знаем. Теоретические сведения, связанные с прогрессиями, впервые встре­чаются в дошедших до нас документах Древней Греции. В «Псаммите» («Исчислении песчинок») Архимед впервые со­поставляет арифметическую и геометрическую прогрессии:


https://multiurok.ru/files/razrabotka-uroka-algebry-chislovaia-posledovatelno.html





Урок №15.

Тема: Решение текстовых задач.

Решите задание на решу ОГЭ по этой ссылке:

https://math-oge.sdamgia.ru/test?id=32612715


Урок №13 - 14.

Тема: Решение текстовых задач.

  1. Задача – это требование или вопрос, на который надо найти ответ, опираясь или учитывая те условия, которые в ней указаны.

  2. Любая задача состоит из трёх частей: условие, объект, требование (вопрос) задачи.

  3. Приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования, каковы условия, исходя из которых надо её решать. Всё это называется анализом задачи.

Весь процесс решения задачи можно разделить на восемь этапов:

1-й этап: анализ;

2-й этап: схематическая запись;

3-й этап: поиск способа решения;

4-й этап: осуществление решения:

5-й этап: проверка решения;

6-й этап: исследование задачи;

7-й этап: формулировка ответа;

8-й этап: анализ решения.

Сначала рассмотрим стандартный вид. Это задачи, для которых имеются общие правила и положения, определяющие точную программу их решения. Сам процесс решения имеет следующие особенности:

  1. Анализ сводится к установлению вида, к которому относится задача.

  2. Поиск решения состоит в составлении последовательности шагов решения задач этого вида.

  3. Само решение стандартной задачи состоит в применении этой общей программы к её условиям.

Но всё-таки, чтобы правильно решать такие задачи, в первую очередь надо определить её вид.

Теперь рассмотрим нестандартные задачи. Исходя из определения стандартных задач, для них не имеется общих правил и положений.

Процесс решения любой нестандартной задачи состоит в последовательном применении двух основных операций:

  1. Переформулировка нестандартной задачи к другой, ей эквивалентной, но уже стандартной.

  2. Разбиение нестандартной задачи на несколько стандартных подзадач.


По типам задачи делятся: «на части и проценты», «на работу», «на движение», «на смеси и сплавы», «на пропорциональность» и т. д.

Задачи «на проценты».

Процентом числа называется его сотая часть.

Решение любых задач на проценты сводится к основным трем действиям с процентами:

-нахождению процентов от числа (умножением на процент выраженный числом);

-нахождению числа по его процентам (делением на процент выраженный числом);

-нахождению процентного отношения чисел (делением части на целое с переводом этого числа в проценты).

Задачи «на работу» делятся на два вида: на производительность труда и на производительность различных механизмов (труб, насосов и т. д.). Такие задачи часто вычисляются по формуле:

А=Pt

где P – производительность труда, т. е. часть работы, выполняемая в единицу времени;

t – время, необходимое для выполнения всей работы.

Пусть Pt=1 – взаимообратные величины, т. е. вся работа А=1, следовательно:

hello_html_m65966bfb.gifhello_html_de267f9.gif

Все задачи на работу решаются по одной общей формуле А=Ptи в большинстве случаев решаются путём составления систем уравнений.

Задачи «на движение».

Надо помнить, что путь равен произведению скорости на время; относительность скоростей тел движущихся в одном направлении (вычитаем), в противоположных (складываем); движение по реке: по течению (собственная скорость +скорость течения); против течения (собственная скорость - скорость течения).

Задачи «на смеси и сплавы».

Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды. В задачах такого типа эти операции приходится проводить мысленно и выполнять расчёты.

При решении задач на смеси считается, что рассматриваемые смеси однородны: не делается различия между литром как единицей массы и как единицей ёмкости. Концентрацией вещества называется отношение массы этого вещества к массе всей смеси (раствора, сплава). Концентрация вещества, выраженная в процентах, называется процентным отношением вещества в смеси (растворе, сплаве).При решении таких задач следует учитывать, что никаких химических процессов, влияющих на количественные соотношения задачи, не происходит.


В задачах «на сплавы» как и в задачах «на смеси» идёт речь о соединении различных веществ, но отличие состоит в том, что эти вещества – металлы. Решать задачу удобно путём составления таблицы, помогающей зрительно воспринимать задачу. Задачи «на смеси и сплавы» решаются множеством способов, но в них всегда присутствует концентрация (доля содержания одного вещества в другом), и они всегда решаются путём составления уравнений.

Задачи «на прямую и обратную пропорциональность».

Эти задачи решаются с помощью составления и решения пропорции.


Урок №12.

Тема: Системы неравенств.

Решение систем неравенств

Системой называется запись нескольких неравенств, обозначенная фигурной скобкой, при этом количество и вид неравенств, входящих в систему, может быть любым. Решением системы неравенств является пересечение решений всех неравенств, входящих в эту систему. Например, двойное неравенство f(x) < g(x) < h(x) записывается следующим образом: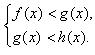Формула Неравества






Урок №11.

Тема: Неравнства.

Неравенством называется выражение, в котором функции соединяются знаками отношения >, <, меньше или равно, больше или равно.Неравенства бывают как числовые, так и буквенные.
Неравенства с двумя знаками отношения, называются двойными, с тремя - тройными и т.д. Например:
a(x) > b(x),
a(x) < b(x),
a(x) меньше или равно b(x),
a(x)  больше или равно b(x).
a(x) < c(x) < b(x) - двойное неравенство.
Неравенства, содержащие знак > или < , называются строгими, а неравенства, содержащие знаки больше либо равно или меньше либо равно - нестрогими.

Решением неравенства является любое значение переменой, при котором это неравенство будет верно.
"Решить неравенство" означает, что надо найти множество всех его решений. Существуют различные методы решения неравенств. Для решения неравенства пользуются числовой прямой, которая бесконечна. 

Свойства неравенств

Выделяют три основных свойства неравенств:

1.      Можно перенести любой член неравенства из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.

2.      Можно умножать или делить обе части неравенства на одно и то же положительное число, при этом знака неравенства не меняется.

3.      Можно умножить или разделить обе части неравенства на одно и то же отрицательное число, при этом знак неравенства меняется на противоположный.

Решение линейных неравенств

Линейным называется неравенство вида ax>b, при этом знак неравенства может быть любым.

Допустим a>0, тогда ax>b равносильно  х>b/a. Решение линейных неравенств, таким образом множество решений неравенства является промежуток (b/a; +бесконечность). Допустим a>0, тогда ax>b равносильно  х< b/a, таким образом множество решений неравенства является промежуток (-бесконечность, b/a).
Если же a=0, тогда 0*x>b, т.е. неравенство не имеет решений при b больше или равно 0, и верно при любых х при b<0.

Решение квадратных неравенств

Квадратным называется неравенство вида ax2 + bx + c > 0, в котром a, b, c – некоторые действительные числа и a не равно 0.

Простейшими квадратными неравенствами являются неравенства x2 < m и x2 > m
Множество решений неравенства x2 < m:

  1. при m< 0 нет чисел, которые в квадрате дают отрицательное число (т.е. нет решений)
при m>0 x принадлежит (-корень из m;+корень из m), т.е. -корень из  m < x  < + корень из m или |x|< корень из m. 
Множество решений неравенства x2 > m:
  1. при m<0 x принадлежит R (т.е. x - любое действительное число);
  2. при m>0 x принадлежит (-бесконечности;-корень из m) объединить с промежутком (+корень из m; +бесконечность), т.е. - бесконечность  < x  < - корень из m  и + корень из  m < x  < + бесконечность или |x|> корень из m.

Решение более сложных квадратных неравенств сводиться к простому переводу выражения вида
ax2 + bx + c > 0
в неравенство
(x-x1)(x-x2) > 0 , где x1 и х2 - корни квадратного уравнения ax2 + bx + c = 0.
Полученное неравенство мы раскладываем таким же образом на систему простых неравенств и легко находим решение.

Решение неравенств методом интервалов

Методом интервалов можно неравенство вида h(x) > 0 (<, больше или равно, меньше или равно ) свести к решению уравнения h(x) = 0.

Данный метод заключается в следующем:

  1. Находится ОДЗ неравенства.
  2. Неравенство приводится к виду h(x) > 0 (<, больше или равно, меньше или равно ) путем упрощения.
  3. Решается уравнение h(x) = 0.
  4. Если на ОДЗ отмечены точки, они ограничивают его и разбивают на интервалы знакопостоянства, при этом знак функции h(х) определяется на каждом таком интервале.
  5. Решением является объединение отдельных множеств, на которых h(x) имеет соответствующий знак. После дополнительной проверки точки ОДЗ, являющиеся граничными, включаются (или не включаются) в ответ.                                                                                                                                                                                                                   Метод интервалов основывается на том, что непрерывная функция h(x) меняет знак либо в граничных точках «разрыва» на ОДЗ, либо при переходе через 0, т.е. в тех точках, которые являются корнями уравнения h(x) = 0. В других точках перемены знака не происходит.

Урок №10.

Тема: Системы уравнений.

        Система уравнений — это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.

             Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться, такую группу уравнений мы называем системой.

      Система уравнений и методы ее решения

  Метод подстановки

         Это самый простой метод, но зачастую – самый трудоемкий. Идея проста – нужно в одном из уравнений выразить одну переменную через другие, а затем полученное выражение подставить в остальные уравнения вместо этой переменной.

          Затем точно так же выражаем и подставляем другую переменную и т.д., пока не получим уравнение с одной переменной.

          После его решения и нахождения одной из переменных последовательно возвращаемся к ранее выраженным, подставляя найденные значения.

Графический метод

     Представить каждое уравнение, входящее в систему в виде зависимости одной переменной от другой (выразив «одну переменную через другую» - задав по сути дела функциональную зависимость). Построить графики этих функций и найти координаты их точек пересечения, эти координаты и будут решением системы.

Метод сложения

Метод сложения основан на следующем: если сложить левые части двух (или больше) уравнений, полученное выражение будет равно сложенным правым частям этих же уравнений. То есть:


{a=b;  c=d ⇒ a+c=b+d

(но ни в коем случае не наоборот: a+c=b+d ◃≠▹ {a=b; c=d)

Действительно, мы ведь имеем право прибавить к обеим частям уравнения одно и то же число, например, прибавим к первому уравнению число c:

{a=b;  c=d ⇒ a+c=b+c

Но раз c=d, в правой части можем заменить c на d:

{a=b; c=d ⇒ a+c=b+c ⇒ a+c=b+d.

https://youclever.org/book/sistemy-uravnenij-1/

Задание на решу ОГЭ по теме занятия:

https://math-oge.sdamgia.ru/test?id=31497531

Урок №9.

Тема: Уравнения.

        Любое равенство вида 

 некоторые функции называются уравнением с одной переменной (или с одной неизвестной).
        Число a называется корнем (или решением) данного уравнения с одной переменной, если при подстановке числа a вместо x в обе части уравнения, получаем верное числовое неравенство, то есть при подстановке x = a обе части уравнения определены и их значения совпадают:

        Решить уравнение – это значит найти все его корни или доказать что их нет.
       ОДЗ называется пересечение множеств областей определения функций 

      Два уравнения называются равносильными, если все корни уравнения первого являются корнями второго и наоборот, все корни второго уравнения являются корнями первого. Если все корни одного уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения. Равносильные (тождественные) преобразования уравнений: 
  • к обеим частям уравнения прибавить любую функцию, которая определена при всех значениях из ОДЗ. Следствие. Члены уравнения можно переносить из одной части уравнения в другую;
  • обе части уравнения умножить на любую функцию, определенную и отличную от нуля при всех допустимых значениях неизвестного. Также можно делить и умножать на число, отличное от нуля;
  • в обеих частях уравнения стоят функции, принимающие только неотрицательные значения, то при возведении в одну и ту же четную степень получаем уравнение, равносильное данному. Появлению “посторонних корней” приводят преобразования:
    а) приведение подобных членов – происходит расширение ОДЗ;
    б) сокращение дроби на выражение, содержащие неизвестное (тоже происходит расширение ОДЗ);
    в) умножение на выражение, содержащее неизвестное;
    г) освобождение дроби от знаменателя, содержащего неизвестное. Необходимо обязательно делить проверку или лучше перейти к смешанной системе.
Виды уравнений: 
а) Линейное;
б) квадратное;
в) уравнение высших порядков (биквадратным, возвратное, симметрическое);
г) уравнения содержащие модуль;
д) уравнение с параметром.
          Методы решения уравнений:
1.  Метод решения – группировка. Если левая часть уравнения представлена в виде разложения на линейные множители, а в правой – число и выносящиеся: (x + a)(x + b)(x + b)(x + c) = A и a + b = c + d, в этом случае возможна группировка множителей.
2. Уравнение с модулем:  а) находим нули модуля; б) дискриминант уравнения разбиваем на промежутки; в) раскрываем модуль на каждом из промежутков; г) выбираем ответ, учитывая данный промежуток; д) ответ – совокупность решений.
3.  ax² + 3ax – (a + 2) = 0 – это квадратное уравнение с параметром. При решении уравнения с параметрами необходимо выяснить, при каких значениях параметров уравнение имеет корни и сколько их в зависимости от параметров при которых это выражение действительно определяет корни уравнения, то есть найти при каком значении параметра: 

 г) x – единственный корень.

Задание на решу ОГЭ по теме занятия:

Урок №8.

Тема: Свойства квадратных корней и их применение в вычислениях.

         Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа a называется такое неотрицательное число, квадрат которого равен а  (√а=x, x2=a; x, a≥0).

       Число или выражение под знаком корня должно быть неотрицательным!

      Необходимо запомнить, что знаки "плюс-минус" являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

         Если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

        Для упрощения записи иррациональных чисел и было введено понятие квадратного корня.


       Внесение множителя под знак корня и вынесение множителя из под знака корня.

         Надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.


Сравнение корней.

        Надо внести множители под знак корня и сравнить подкоренные выражения.

Извлечение корней из больших чисел.


Или разбить число под корнем на множители и извлекать корень из каждого множителя, где это возможно.

https://youclever.org/book/kvadratnyj-koren-1/

Задание на сайте решу ОГЭ по теме занятия:

https://math-oge.sdamgia.ru/test?id=31205734


Урок №7.

Тема: Многочлены.

Итак, повторим ещё раз, что мы  знаем про многчлены:
  1. Многочлен и его стандартный вид
    2.  Сложение и вычитание многочленов
    3. Умножение одночлена на многочлен
    4. Вынесение общего множителя за скобки
    Задание на сайте решу ОГЭ по теме занятия:              https://math-oge.sdamgia.ru/test?id=31101910


Урок №6.

Тема: Многочлены.

         Многочленом называется сумма одночленов.Одночлены, из которых состоит многочлен, называют членами многочлена.Если какой-нибудь многочлен содержит обычное число, то это число называют свободным членом многочлена. 

           Подобные слагаемые в многочлене называют подобными членами многочлена, а приведение подобных слагаемых в многочлене — приведением его подобных членов.

Подобные члены многочлена это члены, имеющие одинаковую буквенную часть.

Многочленом стандартного вида называется многочлен, все члены которого имеют стандартный вид и среди них нет подобных.

Степенью многочлена стандартного вида называют наибольшую из степеней, входящих в него одночленов.

  1. Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить.


  1. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

                      (а + b) (с + d) = ac + ad + bc + bd



Разложить многочлен на множители – значит представить его в виде произведения одночленов и многочленов.

Вынесение общего множителя за скобки, если он есть. Это требование можно выполнить, если найти наибольший общий делитель (НОД) модулей коэффициентов исходных членов. Этот НОД станóвится коэффициентом общего множителя, выносимого за скобки. А буквенную часть общего множителя выбирают так, чтобы члены в скобках не имели общих буквенных множителей. 


Второй способ: способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов так, чтобы в каждой группе можно было вынести за скобки один и тот же множитель.


Третий способ: использование формул сокращённого умножения.


И ещё один способ разложения многочленов на множители – это выделение полного квадрата. Осуществляется он с помощью формул суммы и разности двух выражений.


hello_html_1e231ec0.gif


http://spacemath.xyz/mnogochleny/

https://nsportal.ru/shkola/algebra/library/2015/12/13/posobie-dlya-uchashchihsya-povtorenie-mnogochleny

https://infourok.ru/oporniy-konspekt-po-algebre-mnogochleni-klass-3029519.html


Задание на сайте Решу ОГЭ по теме занятия:

https://math-oge.sdamgia.ru/test?id=31006040


Урок №5.

Тема: Степень с целым показателем и её свойства.

       
    Под степенью некоторого числа "а" с некоторым показателем "n" понимают произведение числа "а" само на себя "n" раз. 
        Когда говорят о степени с целым показателем, это означает, что число "n" должно быть величиной не дробной.

 Возвести число в натуральную степень n — значит умножить число само на себя n раз:
an=a⋅a⋅a⋅...an .

Любое число в первой степени равно самому себе: a1=a


Любое число в нулевой степени равно единице:

a0=1, a≠0С





Свойства степени с целым показателем:






          В физике применяют расчеты степеней с целым показателем для чисел, записанных в стандартном виде:

Задание по теме занятия с сайта Решу ОГЭ:


Урок №4.

Тема: Алгебраические выражения.

Сегодня мы вспомним все виды  преобразований алгебраических выражений:

  1.  Приведение подобных слагаемых.
  2. Разложение на множители.
  3. Сокращение дроби.
  4. Сложение и вычитание дробей. Приведение дробей к общему знаменателю.
  5. Умножение и деление дробей.

    А теперь еще раз вспомним правила к каждому вышеуказанному способу преобразования:

1.     Подобные – это слагаемые (одночлены) с одинаковой буквенной частью. Привести подобные – значит сложить несколько подобных слагаемых друг с другом и получить одно слагаемое. Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и приписать буквенную часть.

2.     После того как ты привел подобные, чаще всего полученное выражение нужно разложить на множители, то есть представить в виде произведения. Особенно это важно в дробях: ведь чтобы можно было сократить дробь, числитель и знаменатель должны быть представлены в виде произведения. Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.

Пять способов разложения многочлена на множители:

А) Вынесение общего множителя за скобки:

Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить:

ac+bc=c(a+b)

Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку. А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.

Делится на:

Признак делимости числа на данный делитель:

2

Оканчивается на: 0, 2, 4, 6, 8

3

Сумма цифр делится на 3

4

Две последние цифры делятся на 4

5

Последняя цифра 0 или 5

7

Разность между числом десятков и удвоенной цифрой единиц делится на семь

9

Сумма цифр делится на 9

10

Последняя цифра – ноль

11

Разность между суммой цифр, стоящих на нечетных местах, и суммой цифр стоящих на четных местах, делится на 11

У математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!

Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением! 

 

Б) Использование формул сокращенного умножения:

Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение. Дальше приведены формулы:

1.    (a+b)2=a2+2ab+b2

2.    (a−b)2=a2−2ab+b2

3.    a2−b2=(a−b)(a+b)

4.    (a+b)3=a3+3a2b+3ab2+b3

5.    (a−b)3=a3−3a2b+3ab2−b3

6.    a3+b3=(a+b)(a2−ab+b2)

 7.    a3−b3=(a−b)(a2+ab+b2)  

           В) Метод группировки:

       Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.

        Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.

 Здесь, например, можно переставить второй член на другое место:


           x3−5x2y−3xy+15y2
              Группируем члены парами, получаем:

             (x3−5x2y)−(3xy−15y2)
             x2(x−5y)−3y(x−5y)
              (x2−3y)(x−5y)

         После разложения должно остаться только умножение!

           Г) Метод выделения полного квадрата:

      Необходимо преобразовать имеющийся многочлен, представив

одно   из  его слагаемых в виде суммы или разности двух членов. Надо увидеть формулы сокращенного умножения, даже если они не присутствуют  целиком,  определить, чего здесь не хватает до полной формулы, и видеть какой член на какие разбивать слагаемые.

х2-4х+2= х2 -4х+4 - 2= (х-2)2-2    

Д)    Разложение квадратного трехчлена на множители:
Квадратный трехчлен – многочлен вида ах2+bx+с=0, где  х –неизвестное, a, b,c– некоторые числа, причем a≠0.

      Значения переменной x, которые обращают квадратный трехчлен в

ноль, называются корнями трехчлена. Следовательно, корни трехчлена –

это корни квадратного уравнения ах2 +bx+c=0.

Если квадратное уравнениеaх2+bx+c=0 имеет корни x1, x2, то его можно записать в виде: aх2+bx+c=a(x−х1)(x−х2).       
                                        

3.     Числитель и знаменатель дроби можно умножать или делить на одно и то же ненулевое число, от чего величина дроби не изменяется.

Чтобы сократить дробь, нужно:

          А) числитель и знаменатель разложить на множители;

Б) если в числителе и знаменателе есть общие множители, их можно вычеркнуть.

Сократить – это значит поделить числитель и знаменатель на одно и то же число. Сокращать можно только множители.


4  Сложение и вычитание обычных дробей – операция хорошо знакомая: ищем ий знаменатель, домножаем каждую дробь на недостающий множитель и складываем/вычитаем числители.  

Чтобы привести дробь к новому знаменателю:                                                                                                       

раскладываем знаменатели на множители;

определяем общие (одинаковые) множители;

выписываем все общие множители по одному разу;

домножаем их на все остальные множители, не общие.

 

·         Если в разных знаменателях есть один и тот же множитель в разной степени, то в общем знаменателе такой множитель будет в максимальной из этих степеней. Когда приводишь дроби к общему знаменателю, пользуйся только операцией умножения!

5.      При делении на дробь, дробь – делитель заменяем на обратную ей дробь (переворачиваем), а действие деление заменяем на действие умножения.

•        Если есть подобные, их надо немедленно привести. В какой бы момент у нас ни образовались подобные, их желательно приводить сразу.

•        То же самое касается сокращения дробей: как только появляется возможность сократить, ей надо воспользоваться. Исключение составляют дроби, которые ты складываешь или вычитаешь: если у них сейчас одинаковые знаменатели, то сокращение нужно оставить на потом.

https://youclever.org/book/razlozhenie-na-mnozhiteli-2/

https://youclever.org/book/preobrazovanie-vyrazhenij-1/

 Задание с сайта Решу ОЕГЭ по теме данного занятия:


Урок №3.

Тема: Алгебраические выражения.


        Числовым выражением называют всякую запись из чисел, знаков арифметических действий и скобок, составленную со смыслом.

         Алгебраическим выражением называется запись из букв, знаков арифметических действий, чисел и скобок, составленная со смыслом.

            Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т. е. можно менять значения букв), эти буквы называют переменными.

           Алгебраические выражения могут быть очень громоздкими, и алгебра учит их упрощать, используя правила, законы, свойства, формулы.

           При упрощении вычислений часто используются законы сложения и умножения.

 

Законы сложения

1)  От перемены мест слагаемых сумма не изменяется, т. е.   a+b=b+a — переместительный закон сложения.

2) Чтобы к сумме двух слагаемых прибавить третье слагаемое, можно к первому слагаемому прибавить сумму второго и третьего слагаемых, т. е.(a+b)+c=a+(b+c) — сочетательный закон сложения.

Законы умножения

1) От перемены мест множителей произведение не меняется, т. е.a⋅b=b⋅a — переместительный закон умножения.

2) Произведение не зависит от группировки его сомножителей, т. е.(a⋅b)⋅c=a⋅(b⋅c) — сочетательный закон умножения.

3) Произведение суммы нескольких чисел на какое-нибудь число равно сумме произведений каждого слагаемого на это число, т. е.  (a+b)⋅c=ac+bc — распределительный закон умножения относительно сложения.

А на ноль делить нельзя!

Вывод:

если при конкретных значениях букв алгебраическое выражение имеет числовое значение, то указанные значения переменных называют допустимыми;

если же при конкретных значениях букв алгебраическое выражение не имеет смысла, то указанные значения переменных называют недопустимыми.

         Подобные – это слагаемые (одночлены) с одинаковой буквенной частью.

Например, в сумме 2ab+3ab+b подобные слагаемые – это 2ab и 3ab.

         Привести подобные – значит сложить несколько подобных слагаемых друг с другом и получить одно слагаемое.

          Чтобы сложить (привести) подобные слагаемые, надо сложить их коэффициенты и приписать буквенную часть.

          После того как ты привел подобные, чаще всего полученное выражение нужно разложить на множители, то есть представить в виде произведения.

Особенно это важно в дробях: ведь чтобы можно было сократить дробь, числитель и знаменатель должны быть представлены в виде произведения.

      Если числитель и знаменатель содержат одинаковые множители, их можно сократить, то есть убрать из дроби.

      Числитель и знаменатель дроби можно умножать или делить на одно и то же  ненулевое число, от чего величина дроби не изменяется.

         

            То есть суть операции сокращения в том, что числитель и знаменатель дроби делим на одно и то же число (или на одно и то же выражение).

Чтобы сократить дробь, нужно:

1.         1. числитель и знаменатель разложить на множители;

2.         2. если в числителе и знаменателе есть общие множители, их можно вычеркнуть.

      Сократить – это значит поделить числитель и знаменатель на одно и то же число. Сокращать можно только множители.

           Арифметическое действие, которое выполняется последним при подсчете значения выражения, является «главным».

          То есть, если ты подставишь вместо букв какие-нибудь (любые) числа, и попытаешься вычислить значение выражения, то если последним действием будет умножение – значит, у нас произведение (выражение разложено на множители).

         Если последним действием будет сложение или вычитание, это значит, что выражение не разложено на множители (а значит, сокращать нельзя).

Приведение дробей к общему знаменателю.

·         раскладываем знаменатели на множители;

·         определяем общие (одинаковые) множители;

·         выписываем все общие множители по одному разу;

·         домножаем их на все остальные множители, не общие.

 

      Если в разных знаменателях есть один и тот же множитель в разной степени, то в общем знаменателе такой множитель будет в максимальной из этих степеней.

Формулы сокращенного умножения:

 (a+b)2 =a2+2ab+b2

(a−b)2=a2−2ab+b2

 а2−b2=(a−b)(a+b)

 (a+b)3=a3+3a2b+3ab2+b3

 (a−b)3=a3−3a2b+3ab2−b3

  а3+b3=(a+b)(a2−ab+b2)

  a3−b3=(a−b)(a2+ab+b2)

 

Два полезных совета:

·         Если есть подобные, их надо немедленно привести. В какой бы момент у нас ни образовались подобные, их желательно приводить сразу.

·         То же самое касается сокращения дробей: как только появляется возможность сократить, ей надо воспользоваться. Исключение составляют дроби, которые ты складываешь или вычитаешь: если у них сейчас одинаковые знаменатели, то сокращение нужно оставить на потом.

             Эта ссылка на задания, выполнение которых проверит, усвоили ли вы этот материал.

https://math-oge.sdamgia.ru/test?id=30804838


Ссылки на источники информации:


 Урок №2.

Тема: Измерения, приближения, оценка.

           Ребята, сегодня у нас тема, которая содержит обширный материал. Вот, основные понятия темы и примеры применения ее к решению задач. Постарайтесь разобраться и вспомнить материал, изученный в 5 - 8 классах.

























 А теперь вспомнив все основные правила и понятия, давайте пройдем по этой ссылке и попробуем справиться с предложенными заданиями:







Урок №1.

Структура и особенности КИМов

       В реформированных КИМах ОГЭ 2021 года по предмету «математика», представленных ФИПИ, 26 заданий будут разделены на две части.

Часть

Кол-во вопросов

Особенности

І

20

Краткий ответ (цифра, число или последовательность чисел)

ІІ

6

Развернутый ответ

При этом 20 заданий будут базового уровня сложности, 4 – повышенного и только 2 – высокого.

Из них условно:

  • к модулю «геометрия» относятся №16-20 и 24-26;
  • к практическому модулю – №1-5;
  • к модулю «алгебра» – № 6-15 и 21-23.

В 2021 году ОГЭ по математике будет охватывать такие основные темы:

№

Тема

Кол-во вопросов

1

Числа и вычисления

7

2

Геометрия

5

3

Алгебраические выражения

2

4

Уравнения и неравенства

2

5

Числовые последовательности

1

6

Функции и графики

1

7

Координаты на прямой и плоскости

1

8

Статистика и теория вероятностей

1

 

В ОГЭ по математике 2021 года в 1 части наряду с новыми задачами встретятся и хорошо знакомые задания, которые эксперты ФИПИ решили оставить без изменений. В частности, неизменными будут задачи на работу с:

  • числовой прямой и координатной плоскостью;
  • формулами (подстановка значений);
  • графиками функций (чтение и построение);
  • уравнениями и неравенствами;
  • вычислениями (на арифметические действия);
  • геометрическими фигурами.

     По мнению экспертов и педагогов, первая часть ОГЭ по математике после реформирования не стала существенно сложнее, хотя ученикам, которые в 2021 году будут заканчивать 9 класс стоит уделить особе внимание новому блоку заданий.

        Вторая часть КИМа также претерпела ряд изменений. Изменены формулировки некоторых задач, а также добавлены элементы прикладной математики с практической направленностью. В сравнении с задачами повышенного и высокого уровня сложности 2019 года, обновленный блок билетов 2021 года выглядит несколько сложнее.

          Конечно, если  вполне удовлетворитесь оценкой «3», то решать 2-ю часть не обязательно. Но для выпускников, которые стремятся получить высокий балл, задания № 21-26 просто необходимы, ведь они дают 37,5% всех первичных баллов.

Какими будут задания?

           Ни для кого не секрет, что работа по математике включает 3 блока, в частности вопросы по геометрии и алгебре, а еще реальной математике. Естественно, задания в тестах следуют друг за другом, не по каким-либо критериям, а просто по уровню сложности. Первостепенно идет базовый показатель сложности. За любое выполненное задание начисляется 1 балл. 

           Следующая часть немного сложнее, важно не просто ответить, но и продемонстрировать ход решения. В реальной математике нет никаких частей, официально к выполнению предложено 7 заданий.

             По установленным нормам  ФИПИ,  ради сдачи ОГЭ хотя бы на оценку 3, следует набрать 8 первичных баллов.

Оценивание ОГЭ по математике

Выполнив идеально все 26 заданий, экзаменуемый в 2021 году может набрать на ОГЭ по математике 32 первичных балла.

При этом каждое задание І части (с 1 по 20) оценивается в 1 б., а каждое задание ІІ части (с 21 по 26) – в 2 б.

Результат ГИА-9 оказывает непосредственное влияние на итоговую оценку, которая формируется из годовой оценки по предмету и оценки, в которую переводят баллы ОГЭ. Для математики ФИПИ предлагает такую таблицу соответствия:

Оценка

Первичные баллы

5

22-32

4

15-21

3

8-14

не сдал

0-7

 

            При переводе баллов в оценку принимают во внимание количество решенных задач по геометрии.
            Так, если экзаменуемый набрал менее 2 б. по геометрическим задачам, выставляют оценку на бал ниже, чем рекомендует таблица соответствия.

          Это значит, что для получения аттестата мало просто набрать 8 первичных баллов – необходимо чтобы минимум 2 из них были за задания из блока «геометрия» (№16-20 или 24-26). Тот же принцип действует и для оценок «4» или «5», поэтому стоит уделить особе внимание данному виду вопросов и задач.

         Для профильных классов и колледжей на 2021 год рекомендованы такие пороговые значения первичных баллов:

  • физико-математический профиль и сфера IT – 19 б.;
  • экономика – 18 б.;
  • естественные науки – 18 б.

 https://god2021bull.com/oge-po-matematike-v-2021-godu-fipi-izmeneniya-podgotovka/

Тема занятия:   Натуральные, рациональные  и действительные числа. Дроби.

           Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей.  Нет, ноль не является натуральным числом. Существует бесконечное множество натуральных чисел. Единица — это наименьшее натуральное число. Сумма натуральных чисел есть натуральное число. Произведение натуральных чисел есть натуральное число. Разность натуральных чисел не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет. Частное натуральных чисел не всегда есть натуральное число. Каждое натуральное число делится на единицу и на себя. Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду  делятся нацело. Единицу не считают простым числом. Числа, которые больше единицы и которые не являются простыми, называют составными. Единицу не считают составным числом. Множество натуральных чисел составляют единица, простые числа и составные числа.  Множество натуральных чисел обозначается латинской буквой N.

                Целые числа — это натуральные числа, ноль и числа, противоположные натуральным. Числа, противоположные натуральным — это целые отрицательные числа. Множество целых чисел обозначается латинской буквой Z.

          Рациональные числа — это целые числа и дроби.  Любое рациональное число может быть представлено в виде периодической дроби. Любое целое число есть периодическая дробь с периодом ноль. Любое рациональное число может быть представлено в виде дроби m/n, где m целое число, n натуральное число. Множество рациональных чисел обозначается латинской буквой Q.

            Иррациональные числа — это бесконечные непериодические десятичные дроби. Действительные числа – это все рациональные и все иррациональные числа. Множество действительных чисел обозначается латинской буквой R.

      Свойства сложения и умножения  чисел:

переместительное свойство сложения

a + b = b + a;

сочетательное свойство сложения

(a + b) + c = a + (b + c);

переместительное свойство умножения

ab = ba;

сочетательное свойство умножения

(ab) c = a (bc);

распределительное свойство умножения

a (b + c) = ab + ac;

               Дробь в математике — число, состоящее из одной или нескольких равных частей (долей) единицы. По способу записи дроби делятся на два формата: обыкновенные  и десятичные.

             Дробью или обыкновенной дробью называется число, состоящее из одной или нескольких равных частей (долей) единицы. Число, которое стоит над чертой дроби, называется числителем, а число, записанное под чертой дроби - знаменателем. Если числитель дроби меньше, чем ее знаменатель, то дробь называется правильной. Дробь,  числитель которой  либо равен, либо больше знаменателя,  называется  неправильной. Сумму натурального числа и правильной дроби обычно записывают без знака плюс. Такие дроби называются смешанными. Натуральное число называют целой частью смешанного числа, а правильную дробь - дробной частью смешанного числа. Если числитель и знаменатель дроби нельзя сократить на одно и тоже число, отличное от 1, то дробь называется несократимой; иначе - сократимой. Если знаменателем дроби являются числа 10, 100, 1000 и т.п., то такая дробь называется десятичной. Составной дробью называется выражение, которое содержит несколько черт дроби.

 https://sbp-program.ru/shkolnaya-algebra/chisla.htm

https://www.webmath.ru/poleznoe/formules_12_1.php

 

        А теперь вспомнив все основные правила и понятия, давайте пройдем по этой ссылке и попробуем справиться с предложенными заданиями:

 https://math-oge.sdamgia.ru/test?id=30671556

 

 

 







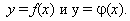
Комментариев нет:

Отправить комментарий

Подписаться на: Сообщения (Atom)